Prerequisites

• Human Level Control Through Deep Reinforcement Learning [Paper]
• Rainbow: Combining Improvements in Deep Reinforcement Learning [ArXiv]

Download

• Original Paper
• Annotated Paper

1-2 Introduction and Background

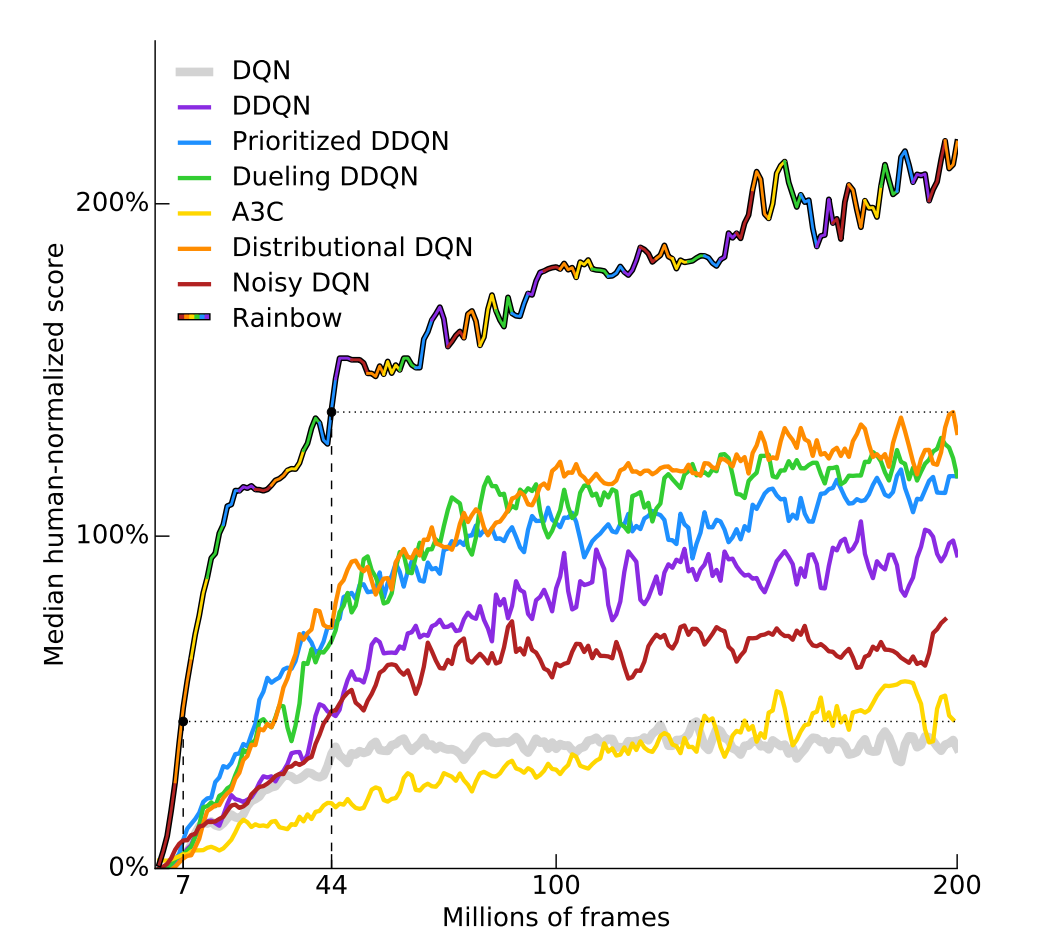
Deep Q-Network (DQN) (Mnih et al., 2015) is one of the most popular deep reinforcement learning (RL) algorithms and has been augmented by various improvements since its formulation. Notably, Rainbow (Hessel et al., 2017) is a collection of popular improvements to DQN.

Deep Q-Network uses an experience replay mechanism, where the agent stores interactions with the environment into a replay buffer and samples minibatches from that buffer during learning. In the original DQN, minibatches were sampled in a uniformly random manner. Since then, various improvements have been introduced. The most popular improvement is prioritized experience replay (Schaul et al., 2015) also included in the Rainbow discussed above. Prioritized experience replay uses the temporal difference (TD) errors of the transitions as their sampling weights to prioritize transitions that are surprising (has high TD error).

Another improvement is combined experience replay (Zhang and Sutton, 2017), which simply includes the most recently added experience to the sampled minibatch. The authors of combined experience replay justify their algorithm by showing that with the original experience replay, performance decreases if the replay capacity (replay buffer size) is too large.

This paper is a continuation of such experiments to understand the effects of hyperparameters related to experience replay. Specifically, the authors focus on disentangling (1) replay capacity, (2) off-policyness of the buffer, and (3) replay ratio.

3 Disentangling Experience Replay

3.1 Independent Factors of Control

First, the paper introduces 4 definitions:

• replay capacity: number of transitions in the buffer
• age of transition: number of gradient updates of the learner since the transition was generated
• age of the oldest policy in the buffer: age of the oldest transition in the replay buffer
• replay ratio: number of gradient updates per environment transition

The age of the oldest policy in the buffer is used as a proxy of the degree of off-policyness of transitions in the buffer.

Note that replay capacity and age of the oldest policy are closely related. For example, increasing the replay capacity increases the age of the oldest policy in the buffer, since the time it takes for a transition to be replaced is directly correlated to the replay capacity.

It is possible to fix one quantity while changing another if we also change the number of transitions per policy. For example, to double the replay capacity while fixing the age of the oldest policy, each policy must generate twice as many transitions. In other words, the policy must be updated with half its frequency, so the replay ratio is halved.

3.2 Experiments

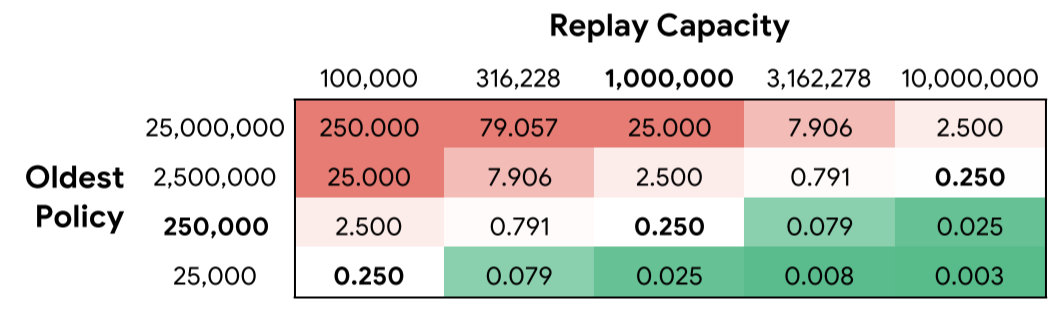
The authors train Rainbow agents with various replay capacity and age of the oldest policy. To independently change each parameter, the replay ratio must be different, as shown below.

For all experiments, the Dopamine implementation of Rainbow is used on 14 games from the Arcade Learning Environment with sticky actions for stochasticity. Note that Dopamine’s implementation of Rainbow differs from the original Rainbow paper in that it only uses prioritized experience replay (PER), Distributional DQN, $n$-step DQN, and Adam optimizer. In other words, it does not use Double DQN, Dueling DQN, and Noisy DQN.

The number of gradient updates and batch size is fixed for a fair comparison of agents. However, note that since the replay ratio is different for each agent, a fixed number of gradient updates means a different number of environment frames are generated.

The figure above shows the median performance improvements. From the figure, the authors observe 3 trends.

Fixing the age of the oldest policy, increasing replay capacity improves performance. Large replay capacity could improve performance since it is less likely to overfit, since the transitions in the replay buffer have more diverse states and actions.

Fixing replay capacity, decreasing the age of the oldest policy improves performance. Decreasing the age of the oldest policy could improve performance since younger transactions are generated with recent agents with more gradient updates, so the agent can spend more time in high-quality regions of the environment.

This second trend is not true when the replay capacity is 10 million transitions. Upon further analysis, the authors observe that the drop in median performance is a result of a sharp performance drop for hard exploration environments (Montezuma’s Revenge and Private Eye).

Fixing replay ratio, increasing replay capacity improves performance. The authors do not provide any hypothesis about this trend.

3.3 Generalizing to Other Agents

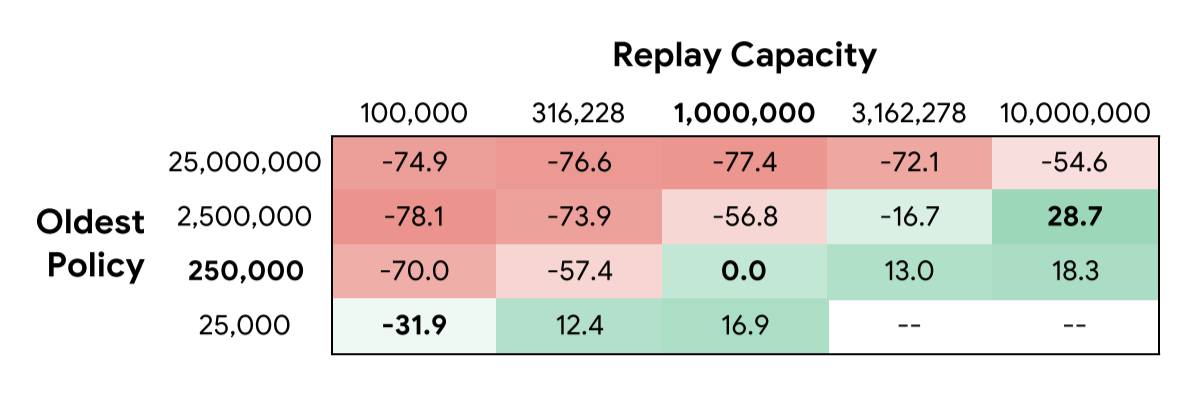
A similar but smaller set of experiments was also done with the original DQN (Mnih et al., 2015). In these experiments, the replay capacity was increased while fixing either the replay ratio or the age of the oldest policy.

As shown in the table above, unlike the Rainbow agent, the original DQN agent does not benefit from increasing the replay capacity. Note that this disagrees with the observation by Zhang and Sutton (2017) that motivated combined experience replay.

4 What Components Enable Improving with a Larger Replay Capacity?

4.1 Additive and Ablative Experiments

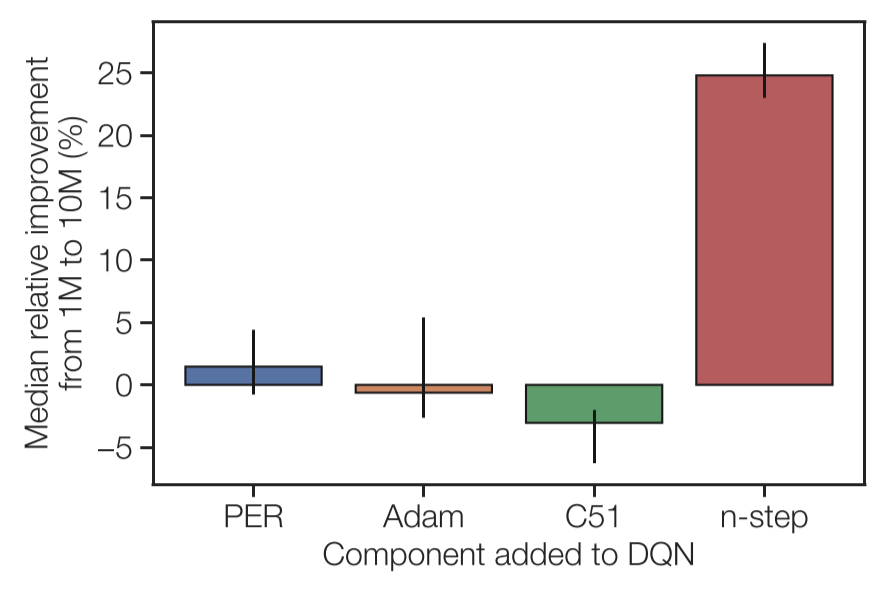
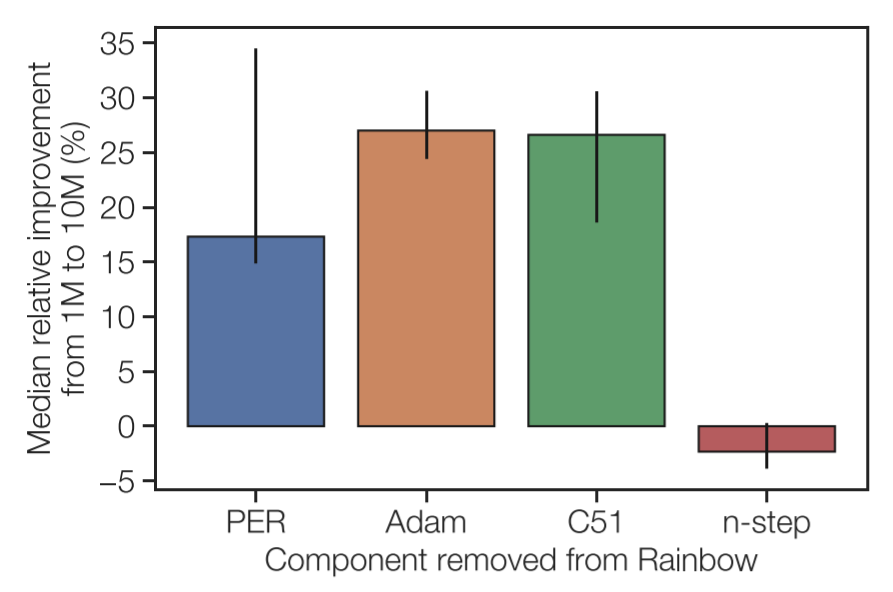
To pinpoint the difference between DQN and Rainbow on increased replay capacity, the authors test the performance of each component of Rainbow independently. The authors perform an additive study, where a single improvement from Rainbow is added to the original DQN, and an ablation study, where a single improvement is removed from the Rainbow DQN.

Dopamine’s implementation of Rainbow consists of four improvements to the original DQN: (1) prioritized experience replay, (2) Adam optimizer, (3) distributional DQN, and (4) $n$-step returns.

The 8 agents are tested across 20 games from the Arcade Learning Environment, including the 14 games used in previous experiments. Each agent is tested with a replay capacity of 1 million and 10 million transitions while fixing the replay ratio.

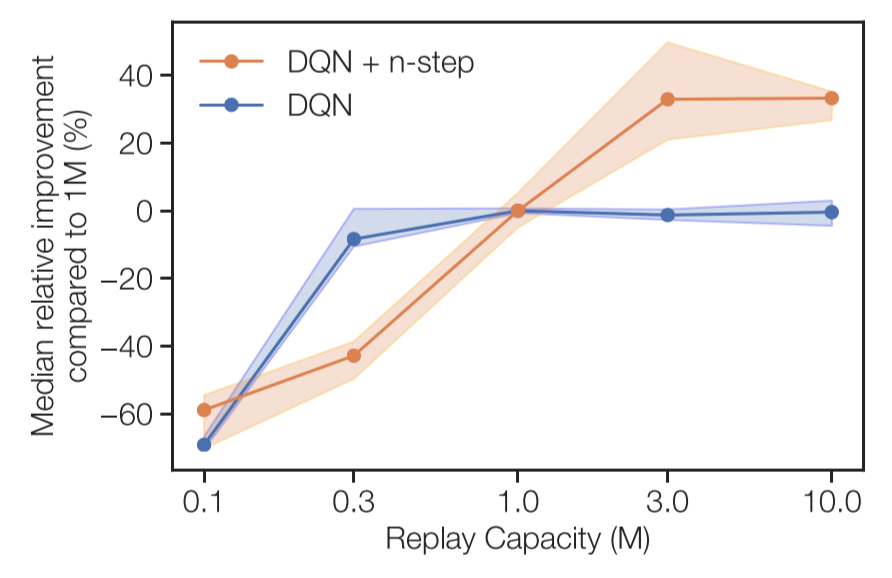
In both studies, $n$-step returns show to be the critical component. Adding $n$-step returns to the original DQN makes the agent improve with larger replay capacity, and removing $n$-step returns to Rainbow makes the agent no longer improve with larger replay capacity.

In a final experiment, the original DQN agent and the DQN agent with $n$-step returns are tested with fixed age of oldest policy (instead of fixed replay ratio) with increasing replay capacity. Again, only the DQN with $n$-step returns increases in performance as the replay capacity increases.

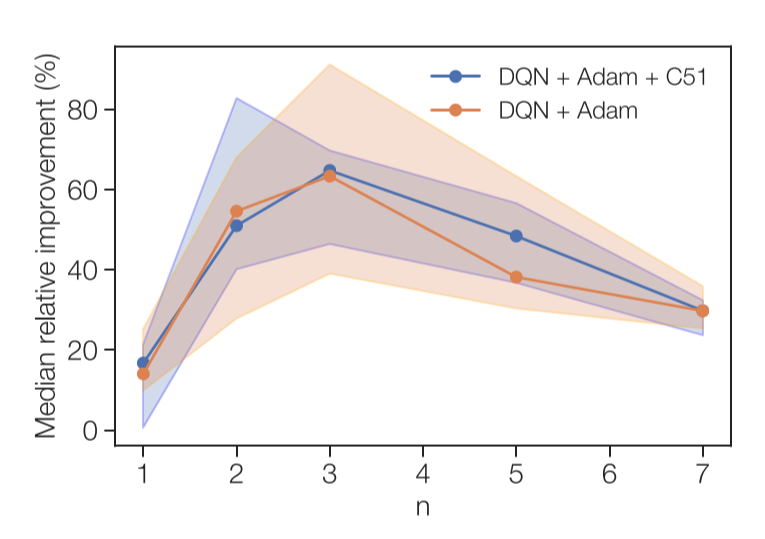
4.2 $n$-step for massive replay capacities

To test the limits of $n$-step returns, the authors also train two agents (DQN + Adam, DQN + Adam + C51) in offline deep reinforcement learning setting, where all data is collected from a separate agent. Both agents are tested with multiple values of $n$ (1, 2, 5, 7).

As expected, performance for $n > 1$ is consistently better than performance without $n$-step returns ($n = 1$).

5 Why is $n$-step the Enabling Factor?

The authors continue by forming two hypotheses on why $n$-step is the component that allows DQN to improve with increased replay capacity.

5.1 Deadening the Deadly Triad

One possible hypothesis is that $n$-step counters the increased off-policyness from increased replay capacity. Off-policyness of the data is known to cause unstable learning or divergence when paired with function approximation and bootstrapping. This is called the “deadly triad”.

If $n$-step returns can alleviate one of the components of the deadly triad, that would explain the enhanced performance. $n$-step returns do not change the function approximation of $Q$-values or the off-policyness of the data, but it is related to bootstrapping. The 1-step target and the $n$-step target are written below:

The bootstrapping factor is the $Q(s, a)$ term at the end. In the $n$-step target, the term is multiplied by $\gamma^n$, whereas in the original $1$-step target, the term is multiplied by $\gamma$. Since $\gamma$ is the discount factor set to be below 1, the $n$-step target is less affected by the term.

If this is what makes $n$-step DQN better than 1-step DQN, then simply using 1-step DQN with $\gamma^n$ as the discount factor should have a similar effect. Unfortunately, no such improvement is observed, invalidating this hypothesis.

Another evidence against the hypothesis is that DQN’s performance does not improve with a larger replay capacity when the age of the oldest policy is fixed. If the age of the oldest policy is fixed, the off-policyness is fixed, so the deadly triad should be the same for any replay capacity. However, DQN’s performance does not increase with increased replay capacity.

5.2 Variance Reduction

Another possible hypothesis is that $n$-step returns benefit from increased replay capacity since it reduces the variance of returns. As $n$ increases, more terms are added to the $n$-step target, increasing the variance of the target return.

Another way to see that increasing $n$ increases the variance of returns is by observing that $n$-step returns are an interpolation between 1-step temporal difference (TD) methods and Monte Carlo (MC) methods. TD methods have low variance and high bias. and MC methods have low bias but high variance. As $n$ increases, the $n$-step return approaches Monte Carlo methods, so it has a lower bias but higher variance.

A bigger replay buffer could alleviate this increased variance from $n$-step returns. With more transitions in the buffer, the expected diversity of transitions in the buffer is increased. Therefore, as the buffer discards and adds new transitions, the distribution of transitions in a larger replay buffer changes less.

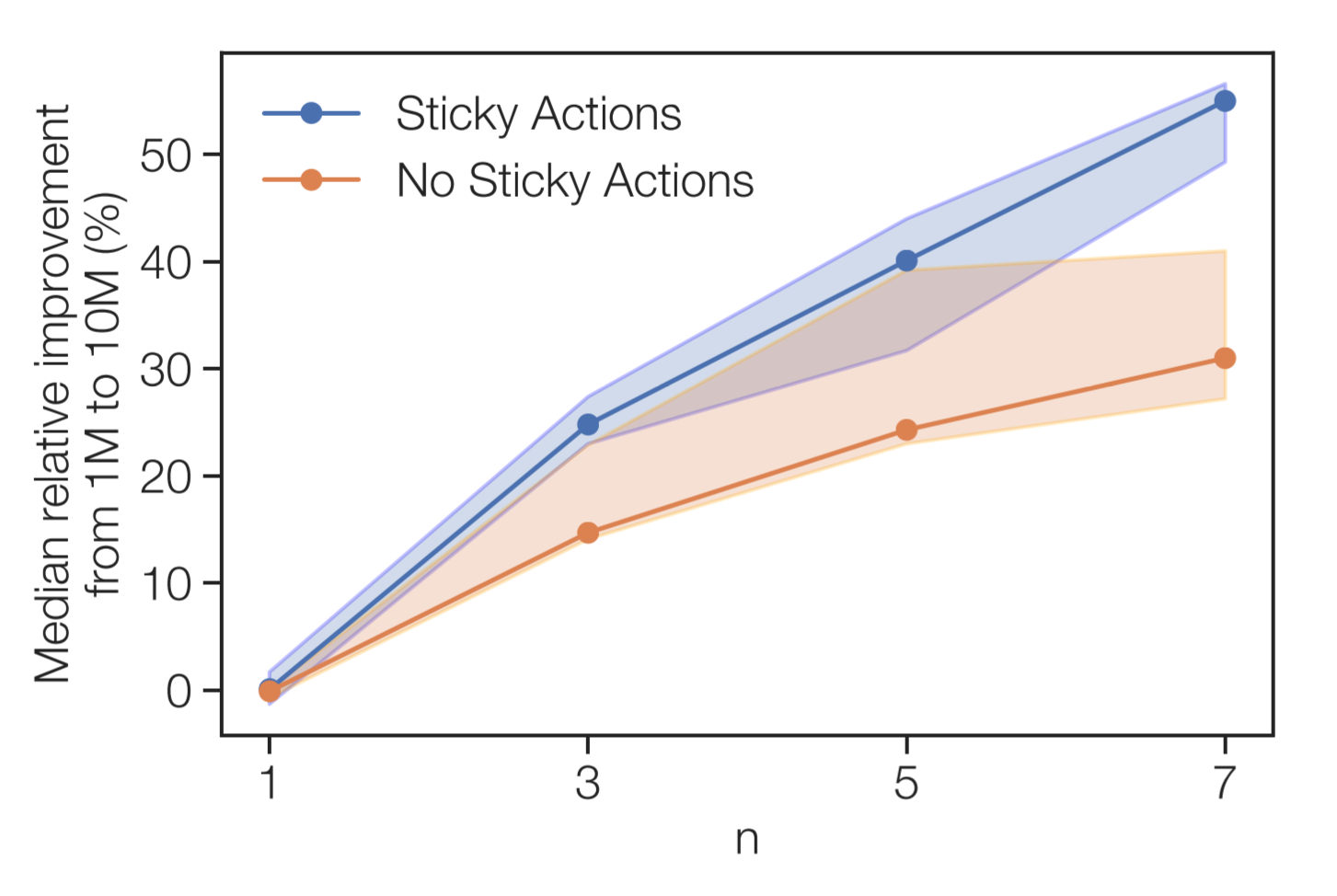
If this hypothesis is true, then removing a source of variance from the environment should lessen the impact of $n$-step returns. One way to reduce the variance is by not using “sticky actions.” Sticky actions introduce stochasticity to the environment by causing previously taken action to be repeated (regardless of the new chosen action) with some probability. Without sticky actions, the Atari game has a lower variance of returns.

The experiment shows that removing sticky actions and reducing variance indeed lowers the impact of $n$-step returns. However, without sticky actions, agents with $n$-step returns still benefit from increased replay capacity. Therefore, although variance reduction is one reason that $n$-step returns benefit from increased replay capacity, it does not provide a full explanation.

5.3 Further Multi-step and Off-policy Methods

The authors simply mention that similar work can be done in the future for more general classes of return estimators using multi-step off-policy data, such as $Q(\lambda)$, TreeBackup, and Retrace.

6 Discussion

To summarize, this paper made the following discoveries and contributions:

• Increasing replay capacity improves performance
• Decreasing age of oldest policy improves performance
• $n$-step returns allow the agent to take advantage of the larger replay capacity
• Increasing replay capacity can mitigate variance of $n$-step returns

In the bigger picture, this paper can be seen as a study on the interaction between learning algorithms (DQN) and data generating mechanisms (experience replay). Although the numerous components of learning algorithms and data generating mechanisms are difficult to control independently, this paper shows that sometimes these properties could be disentangled, giving further insight.