Train Proximal Policy Optimization (PPO) with Swift for TensorFlow (S4TF)

Published Sep 07, 2020 by Seungjae Ryan Lee

Introduction

Proximal Policy Optimization (PPO) is a reinforcement learning algorithm published by OpenAI (Schulman et al.) in 2017. It is a policy gradient algorithm that succeeded Trust Region Policy Optimization (TRPO) with the benefit of being easier to implement without a drop in performance. It has become one of the most commonly used baselines for new reinforcement learning tasks, and its variants have also been used to train a robot hand to solve a Rubik’s cube or win Dota 2 against professional players.

Swift for TensorFlow (S4TF) is Google’s product to bring machine learning to Swift. Python has been the primary language for prototyping and developing machine learning models, with the two most popular machine learning libraries (TensorFlow and PyTorch) both being Python libraries. Python has a great benefit of being easy to use. However, native Python is very slow and relies on external libraries like NumPy for computation. Swift, on the other hand, is faster and safer, while still being easy to use.

In this post, we explore how to use Swift for TensorFlow to implement Proximal Policy Optimization. We look at each component of Proximal Policy Optimization and see how they can be translated to Swift for TensorFlow. The code is also available in GitHub.

This work is a part of my Google Summer of Code project. Google Summer of Code connects student developers with open source organizations. Students are assigned mentors from the organizations to help them contribute to their software. I had the pleasure of working with Brad Larson and Dan Zheng from TensorFlow, and this work would not have been possible without them.

Actor-Critic

Proximal Policy Optimization (PPO) is an Actor-Critic method. As the name suggests, the Actor-Critic system has two models: the Actor and the Critic. The Actor corresponds to the policy $\pi$ and is used to choose the action for the agent and update the policy network. The Critic corresponds to the value function $Q(s, a)$ (for action value) or $V(s)$ (for state value). The Critic updates the parameters of the network for the value function used during the Actor update.

The actor network receives observation (state) as the input and outputs a list of probabilities, with one probability per action. These probabilities form a distribution, and the action can then be chosen by sampling from this distribution.

To represent the state value function, the critic network also receives the state as the input and outputs a single number representing the estimated state value of that state.

We need two neural networks ActorNetwork and CriticNetwork in S4TF using the Layer protocol. During initialization, we define dense layers by their input and output sizes and activation functions. Then, we allow the network to be called as a function using the Tensor.sequenced() function.

Full Code for ActorNetwork struct

/// The actor network that returns a probability for each action.
///
/// Actor-Critic methods has an actor network and a critic network. The actor network is the policy
/// of the agent: it is used to select actions.
struct ActorNetwork: Layer {
    typealias Input = Tensor<Float>
    typealias Output = Tensor<Float>

    var l1, l2, l3: Dense<Float>

    init(observationSize: Int, hiddenSize: Int, actionCount: Int) {
        l1 = Dense<Float>(
            inputSize: observationSize,
            outputSize: hiddenSize,
            activation: tanh,
            weightInitializer: heNormal()
        )
        l2 = Dense<Float>(
            inputSize: hiddenSize,
            outputSize: hiddenSize,
            activation: tanh,
            weightInitializer: heNormal()
        )
        l3 = Dense<Float>(
            inputSize: hiddenSize,
            outputSize: actionCount,
            activation: softmax,
            weightInitializer: heNormal()
        )
    }

    @differentiable
    func callAsFunction(_ input: Input) -> Output {
        return input.sequenced(through: l1, l2, l3)
    }
}

Full Code for CriticNetwork struct

/// The critic network that returns the estimated value of each action, given a state.
///
/// Actor-Critic methods has an actor network and a critic network. The critic network is used to
/// estimate the value of the state-action pair. With these value functions, the critic can evaluate
/// the actions made by the actor.
struct CriticNetwork: Layer {
    typealias Input = Tensor<Float>
    typealias Output = Tensor<Float>

    var l1, l2, l3: Dense<Float>

    init(observationSize: Int, hiddenSize: Int) {
        l1 = Dense<Float>(
            inputSize: observationSize,
            outputSize: hiddenSize,
            activation: relu,
            weightInitializer: heNormal()
        )
        l2 = Dense<Float>(
            inputSize: hiddenSize,
            outputSize: hiddenSize,
            activation: relu,
            weightInitializer: heNormal()
        )
        l3 = Dense<Float>(
            inputSize: hiddenSize,
            outputSize: 1,
            weightInitializer: heNormal()
        )
    }

    @differentiable
    func callAsFunction(_ input: Input) -> Output {
        return input.sequenced(through: l1, l2, l3)
    }
}

We can also create a separate struct called ActorCritic that contains both the ActorNetwork and CriticNetwork. We also use the Layer protocol to call ActorCritic as a function. This function creates and returns a categorical distribution from the output of the actor network. For this Categorical distribution, we borrow code from eaplatanios/swift-rl.

We will use the same layer size for the input layer and the hidden layer. Some implementations have the actor and the critic to share parameters, but we will use different parameters here.

Full Code for Categorical struct

// Below code comes from eaplatanios/swift-rl:
// https://github.com/eaplatanios/swift-rl/blob/master/Sources/ReinforcementLearning/Utilities/Protocols.swift
public protocol Batchable {
  func flattenedBatch(outerDimCount: Int) -> Self
  func unflattenedBatch(outerDims: [Int]) -> Self
}

public protocol DifferentiableBatchable: Batchable, Differentiable {
  @differentiable(wrt: self)
  func flattenedBatch(outerDimCount: Int) -> Self

  @differentiable(wrt: self)
  func unflattenedBatch(outerDims: [Int]) -> Self
}

extension Tensor: Batchable {
  public func flattenedBatch(outerDimCount: Int) -> Tensor {
    if outerDimCount == 1 {
      return self
    }
    var newShape = [-1]
    for i in outerDimCount..<rank {
      newShape.append(shape[i])
    }
    return reshaped(to: TensorShape(newShape))
  }

  public func unflattenedBatch(outerDims: [Int]) -> Tensor {
    if rank > 1 {
      return reshaped(to: TensorShape(outerDims + shape.dimensions[1...]))
    }
    return reshaped(to: TensorShape(outerDims))
  }
}

extension Tensor: DifferentiableBatchable where Scalar: TensorFlowFloatingPoint {
  @differentiable(wrt: self)
  public func flattenedBatch(outerDimCount: Int) -> Tensor {
    if outerDimCount == 1 {
      return self
    }
    var newShape = [-1]
    for i in outerDimCount..<rank {
      newShape.append(shape[i])
    }
    return reshaped(to: TensorShape(newShape))
  }

  @differentiable(wrt: self)
  public func unflattenedBatch(outerDims: [Int]) -> Tensor {
    if rank > 1 {
      return reshaped(to: TensorShape(outerDims + shape.dimensions[1...]))
    }
    return reshaped(to: TensorShape(outerDims))
  }
}

// Below code comes from eaplatanios/swift-rl:
// https://github.com/eaplatanios/swift-rl/blob/master/Sources/ReinforcementLearning/Distributions/Distribution.swift
public protocol Distribution {
  associatedtype Value

  func entropy() -> Tensor<Float>

  /// Returns a random sample drawn from this distribution.
  func sample() -> Value
}

public protocol DifferentiableDistribution: Distribution, Differentiable {
  @differentiable(wrt: self)
  func entropy() -> Tensor<Float>
}

// Below code comes from eaplatanios/swift-rl:
// https://github.com/eaplatanios/swift-rl/blob/master/Sources/ReinforcementLearning/Distributions/Categorical.swift
public struct Categorical<Scalar: TensorFlowIndex>: DifferentiableDistribution, KeyPathIterable {
  /// Log-probabilities of this categorical distribution.
  public var logProbabilities: Tensor<Float>

  @inlinable  
  @differentiable(wrt: probabilities)
  public init(probabilities: Tensor<Float>) {
    self.logProbabilities = log(probabilities)
  }

  @inlinable
  @differentiable(wrt: self)
  public func entropy() -> Tensor<Float> {
    -(logProbabilities * exp(logProbabilities)).sum(squeezingAxes: -1)
  }

  @inlinable
  public func sample() -> Tensor<Scalar> {
    let seed = Context.local.randomSeed
    let outerDimCount = self.logProbabilities.rank - 1
    let logProbabilities = self.logProbabilities.flattenedBatch(outerDimCount: outerDimCount)
    let multinomial: Tensor<Scalar> = _Raw.multinomial(
      logits: logProbabilities,
      numSamples: Tensor<Int32>(1),
      seed: Int64(seed.graph),
      seed2: Int64(seed.op))
    let flattenedSamples = multinomial.gathering(atIndices: Tensor<Int32>(0), alongAxis: 1)
    return flattenedSamples.unflattenedBatch(
      outerDims: [Int](self.logProbabilities.shape.dimensions[0..<outerDimCount]))
  }
}

Full Code for ActorCritic struct

/// The actor-critic that contains actor and critic networks for action selection and evaluation.
///
/// Weight are often shared between the actor network and the critic network, but in this example,
/// they are separated networks.
struct ActorCritic: Layer {
    var actorNetwork: ActorNetwork
    var criticNetwork: CriticNetwork

    init(observationSize: Int, hiddenSize: Int, actionCount: Int) {
        self.actorNetwork = ActorNetwork(
            observationSize: observationSize,
            hiddenSize: hiddenSize,
            actionCount: actionCount
        )
        self.criticNetwork = CriticNetwork(
            observationSize: observationSize,
            hiddenSize: hiddenSize
        )
    }

    @differentiable
    func callAsFunction(_ state: Tensor<Float>) -> Categorical<Int32> {
        precondition(state.rank == 2, "The input must be 2-D ([batch size, state size]).")
        let actionProbs = self.actorNetwork(state).flattened()
        let dist = Categorical<Int32>(probabilities: actionProbs)
        return dist
    }
}

Memory

Like A3C from Asynchronous methods for deep reinforcement learning, PPO saves experience and uses batch updates to update the actor and critic network. The agent interacts with the environment using the actor network, saving its experience into memory. Once the memory has a set number of experiences, the agent updates its networks using all the experience it collected for a set number of epochs. Once the training is finished, the agent clears the memory and starts interacting with the environment with the updated actor network.

Although this may seem similar to the experience replay mechanism in DQN, there are many differences. In DQN, a random minibatch is sampled per update, but in PPO all the experience in memory is used. Also, in DQN’s experience replay, old experiences are removed one-by-one once the. buffer is full, but in PPO, the entire memory is cleared at once after the update is finished.

Finally, PPO stores different components as experience, since its update equation is different. Each experience for PPO consists of five components: the state the agent was in, the action it took, the log probability of the chosen action, the reward it received, and whether the episode finished.

We can create a PPOMemory struct to represent this memory. Each component can be stored separately using Swift arrays, and we can define append() and removeAll() functions to update them.

Full Code for PPOMemory struct

/// A cache saving all rollouts for batch updates.
///
/// PPO first collects fixed-length trajectory segments then updates weights. All the trajectory
/// segments are discarded after the update.
struct PPOMemory {
    /// The states that the agent observed.
    var states: [[Float]] = []
    /// The actions that the agent took.
    var actions: [Int32] = []
    /// The rewards that the agent received from the environment after taking
    /// an action.
    var rewards: [Float] = []
    /// The log probabilities of the chosen action.
    var logProbs: [Float] = []
    /// The episode-terminal flag that the agent received after taking an action.
    var isDones: [Bool] = []

    init() {}

    mutating func append(state: [Float], action: Int32, reward: Float, logProb: Float, isDone: Bool) {
        states.append(state)
        actions.append(action)
        logProbs.append(logProb)
        rewards.append(reward)
        isDones.append(isDone)
    }

    mutating func removeAll() {
        states.removeAll()
        actions.removeAll()
        rewards.removeAll()
        logProbs.removeAll()
        isDones.removeAll()
    }
}

Full Code for PPOAgent.step() for Agent-Environment Interaction

func step(env: PythonObject, state: PythonObject) -> (PythonObject, Bool, Float) {
    let tfState: Tensor<Float> = Tensor<Float>(numpy: np.array([state], dtype: np.float32))!
    let dist: Categorical<Int32> = oldActorCritic(tfState)
    let action: Int32 = dist.sample().scalarized()
    let (newState, reward, isDone, _) = env.step(action).tuple4

    memory.append(
        state: Array(state)!,
        action: action,
        reward: Float(reward)!,
        logProb: dist.logProbabilities[Int(action)].scalarized(),
        isDone: Bool(isDone)!
    )

    return (newState, Bool(isDone)!, Float(reward)!)
}

Update Equation

In policy gradient methods, we use gradient ascent to maximize the objective function. First, we define the probability ratio $r(\theta)$ between old policy $\theta_{old}$ and new policy $\theta$.

\[\color{green}{r(\theta)} = \frac{\pi_\theta(a | s)}{\pi_{\theta_{old}}(a | s)}\]

Note that $r(\theta) > 1$ if the action will be selected more in the new policy, and $r(\theta) < 1$ if the action will be selected less in the new policy. Using this probability ratio, we can create a simple objective function.

\[L^{NAIVE}(\theta) = \mathbb{E}[\color{green}{r(\theta)} \color{darkorange}{\hat{A}_{\theta_{old}}(s, a)}]\]

where $\color{darkorange}{\hat{A}(s, a)}$ is some advantage function. There are multiple options for the advantage function $\color{darkorange}{\hat{A}(s, a)}$. (The paper High-Dimensional Continuous Control Using Generalized Advantage Estimation lists several functions.) In PPO, a truncated version of generalizaed advantage function (GAE) is used:

\[\color{darkorange}{\hat{A}_t} = \delta_t + (\gamma \lambda) \delta_{t + 1} + \ldots + (\gamma \lambda)^{T-t+1} \delta_{T-1}\]

where $\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$.

Instead of GAE, we will use the advantage function from A3C:

\[\color{darkorange}{\hat{A}_t} = -V(s_t) + r_t + \gamma r_{t+1} + \ldots + \gamma^{T-t+1} r_{T-1} + \gamma^{T-t} V(s_T)\]

In S4TF, these advantages are computed per step by iterating backwards through the rewards in the memory and multiplying them by the discount factor.

var rewards: [Float] = []
var discountedReward: Float = 0
for i in (0..<memory.rewards.count).reversed() {
    if memory.isDones[i] {
        discountedReward = 0
    }
    discountedReward = memory.rewards[i] + (discount * discountedReward)
    rewards.insert(discountedReward, at: 0)
}
let advantages: Tensor<Float> = tfRewards - stateValues

We also normalize the advantage function by subtracting by the mean and dividing by the standard deviation added by a small number to ensure numerical stability.

tfRewards = (tfRewards - tfRewards.mean()) / (tfRewards.standardDeviation() + 1e-5)

However, the naive objective function $L^{NAIVE}(\theta)$ can be unstable when the action selection probability is low with the old policy, since $r(\theta)$ is high, making the updates extremely large.

PPO suggests two possible fixes: PPO-Clip and PPO-Penalty. Let’s focus on PPO-Clip since it is more commonly used. PPO-Clip simply clips the probability ratio $r(\theta)$ to constrain the size of the update. The ratio is constrained to be between some interval $(1 - \epsilon, 1 + \epsilon)$, where $\epsilon$ is a clipping hyperparameter. Then, the objective function becomes:

\[\color{blue}{L^{CLIP}(\theta)} = \mathbb{E}\left[ \min\left( \color{green}{r(\theta)} \color{darkorange}{\hat{A}_{\theta_{old}}(s, a)}, \text{clip}(\color{green}{r(\theta)}, 1-\epsilon, 1+\epsilon) \color{darkorange}{\hat{A}_{\theta_{old}}(s, a)} \right) \right]\]

Note that the objective function only uses the policy (actor network). Therefore, we need another term that uses the value function to update the critic network. For the critic network, we seek to minimize the difference between the estimated value and the actual value. Using the squared loss, we get another objective function $L^{VF}(\theta)$:

\[\color{red}{L^{VF}(\theta)} = (V_{\theta} - V^{\text{Target}})^2\]

Finally, we add an entropy term to encourage exploration. Then, the final objective function is:

\[L(\theta) = \color{blue}{L^{CLIP}(\theta)} - c_1 \color{red}{L^{VF}(\theta)} + c_2S[\pi_\theta](s))\]

Note that we want to minimize $\color{red}{L^{VF}(\theta)}$, so we use the negative objective.

In S4TF, we separate the loss into one loss $\color{blue}{L^{CLIP}(\theta)} + c_2S[\pi_\theta](s))$ for the actor network and another loss $\color{red}{L^{VF}(\theta)}$ for the critic network.

For the actor network, we grab the states, actions, and the log probabilities using the old policy from the memory. Then, we compute the log probabilities using the new policy and compute the probability ratio $\color{green}{r(\theta)}$. With this, we compute the advantages, which allows us to compute the loss $\color{blue}{L^{CLIP}(\theta)}$. We also compute the entropy loss for exploration and add the two losses together to get the final loss for the policy update.

// Retrieve stored states, actions, and log probabilities from the old policy
let oldStates: Tensor<Float> = Tensor<Float>(numpy: np.array(memory.states, dtype: np.float32))!
let oldActions: Tensor<Int32> = Tensor<Int32>(numpy: np.array(memory.actions, dtype: np.int32))!
let oldLogProbs: Tensor<Float> = Tensor<Float>(numpy: np.array(memory.logProbs, dtype: np.float32))!
// Optimize policy network (actor)
let (actorLoss, actorGradients) = valueWithGradient(at: self.actorCritic.actorNetwork) { actorNetwork -> Tensor<Float> in
    // Get log probabilities using the new policy
    let npIndices = np.stack([np.arange(oldActions.shape[0], dtype: np.int32), oldActions.makeNumpyArray()], axis: 1)
    let tfIndices = Tensor<Int32>(numpy: npIndices)!
    let actionProbs = actorNetwork(oldStates).dimensionGathering(atIndices: tfIndices)

    // Compute the probability ratio
    let dist = Categorical<Int32>(probabilities: actionProbs)
    let stateValues = self.actorCritic.criticNetwork(oldStates).flattened()
    let ratios: Tensor<Float> = exp(dist.logProbabilities - oldLogProbs)

    // Compute the PPO loss
    let advantages: Tensor<Float> = tfRewards - stateValues
    let surrogateObjective = Tensor(stacking: [
        ratios * advantages,
        ratios.clipped(min:1 - self.clipEpsilon, max: 1 + self.clipEpsilon) * advantages
    ]).min(alongAxes: 0).flattened()
    let entropyBonus: Tensor<Float> = Tensor<Float>(self.entropyCoefficient * dist.entropy())
    let loss: Tensor<Float> = -1 * (surrogateObjective + entropyBonus)

    return loss.mean()
}
self.actorOptimizer.update(&self.actorCritic.actorNetwork, along: actorGradients)

For the critic network, we use the cumulative rewards computed for the objective function as the target. We train the critic network so that its predicted state values match the cumulative rewards.

// Optimize value network (critic)
let (criticLoss, criticGradients) = valueWithGradient(at: self.actorCritic.criticNetwork) { criticNetwork -> Tensor<Float> in
    let stateValues = criticNetwork(oldStates).flattened()
    let loss: Tensor<Float> = 0.5 * pow(stateValues - tfRewards, 2)

    return loss.mean()
}
self.criticOptimizer.update(&self.actorCritic.criticNetwork, along: criticGradients)

These updates are done for multiple epochs, then the memory is discarded. This completes the PPOAgent class.

Full Code for PPOAgent class

/// Agent that uses the Proximal Policy Optimization (PPO).
///
/// Proximal Policy Optimization is an algorithm that trains an actor (policy) and a critic (value
/// function) using a clipped objective function. The clipped objective function simplifies the
/// update equation from its predecessor Trust Region Policy Optimization (TRPO). For more
/// information, check Proximal Policy Optimization Algorithms (Schulman et al., 2017).
class PPOAgent {
    // Cache for trajectory segments for minibatch updates.
    var memory: PPOMemory
    /// The learning rate for both the actor and the critic.
    let learningRate: Float
    /// The discount factor that measures how much to weight to give to future
    /// rewards when calculating the action value.
    let discount: Float
    /// Number of epochs to run minibatch updates once enough trajectory segments are collected.
    let epochs: Int
    /// Parameter to clip the probability ratio.
    let clipEpsilon: Float
    /// Coefficient for the entropy bonus added to the objective.
    let entropyCoefficient: Float

    var actorCritic: ActorCritic
    var oldActorCritic: ActorCritic
    var actorOptimizer: Adam<ActorNetwork>
    var criticOptimizer: Adam<CriticNetwork>

    init(
        observationSize: Int,
        hiddenSize: Int,
        actionCount: Int,
        learningRate: Float,
        discount: Float,
        epochs: Int,
        clipEpsilon: Float,
        entropyCoefficient: Float
    ) {
        self.learningRate = learningRate
        self.discount = discount
        self.epochs = epochs
        self.clipEpsilon = clipEpsilon
        self.entropyCoefficient = entropyCoefficient

        self.memory = PPOMemory()

        self.actorCritic = ActorCritic(
            observationSize: observationSize,
            hiddenSize: hiddenSize,
            actionCount: actionCount
        )
        self.oldActorCritic = self.actorCritic
        self.actorOptimizer = Adam(for: actorCritic.actorNetwork, learningRate: learningRate)
        self.criticOptimizer = Adam(for: actorCritic.criticNetwork, learningRate: learningRate)
    }

    func step(env: PythonObject, state: PythonObject) -> (PythonObject, Bool, Float) {
        let tfState: Tensor<Float> = Tensor<Float>(numpy: np.array([state], dtype: np.float32))!
        let dist: Categorical<Int32> = oldActorCritic(tfState)
        let action: Int32 = dist.sample().scalarized()
        let (newState, reward, isDone, _) = env.step(action).tuple4

        memory.append(
            state: Array(state)!,
            action: action,
            reward: Float(reward)!,
            logProb: dist.logProbabilities[Int(action)].scalarized(),
            isDone: Bool(isDone)!
        )

        return (newState, Bool(isDone)!, Float(reward)!)
    }

    func update() {
        // Discount rewards for advantage estimation
        var rewards: [Float] = []
        var discountedReward: Float = 0
        for i in (0..<memory.rewards.count).reversed() {
            if memory.isDones[i] {
                discountedReward = 0
            }
            discountedReward = memory.rewards[i] + (discount * discountedReward)
            rewards.insert(discountedReward, at: 0)
        }
        var tfRewards = Tensor<Float>(rewards)
        tfRewards = (tfRewards - tfRewards.mean()) / (tfRewards.standardDeviation() + 1e-5)

        // Retrieve stored states, actions, and log probabilities
        let oldStates: Tensor<Float> = Tensor<Float>(numpy: np.array(memory.states, dtype: np.float32))!
        let oldActions: Tensor<Int32> = Tensor<Int32>(numpy: np.array(memory.actions, dtype: np.int32))!
        let oldLogProbs: Tensor<Float> = Tensor<Float>(numpy: np.array(memory.logProbs, dtype: np.float32))!

        // Optimize actor and critic
        var actorLosses: [Float] = []
        var criticLosses: [Float] = []
        for _ in 0..<epochs {
            // Optimize policy network (actor)
            let (actorLoss, actorGradients) = valueWithGradient(at: self.actorCritic.actorNetwork) { actorNetwork -> Tensor<Float> in
                let npIndices = np.stack([np.arange(oldActions.shape[0], dtype: np.int32), oldActions.makeNumpyArray()], axis: 1)
                let tfIndices = Tensor<Int32>(numpy: npIndices)!
                let actionProbs = actorNetwork(oldStates).dimensionGathering(atIndices: tfIndices)

                let dist = Categorical<Int32>(probabilities: actionProbs)
                let stateValues = self.actorCritic.criticNetwork(oldStates).flattened()
                let ratios: Tensor<Float> = exp(dist.logProbabilities - oldLogProbs)

                let advantages: Tensor<Float> = tfRewards - stateValues
                let surrogateObjective = Tensor(stacking: [
                    ratios * advantages,
                    ratios.clipped(min:1 - self.clipEpsilon, max: 1 + self.clipEpsilon) * advantages
                ]).min(alongAxes: 0).flattened()
                let entropyBonus: Tensor<Float> = Tensor<Float>(self.entropyCoefficient * dist.entropy())
                let loss: Tensor<Float> = -1 * (surrogateObjective + entropyBonus)

                return loss.mean()
            }
            self.actorOptimizer.update(&self.actorCritic.actorNetwork, along: actorGradients)
            actorLosses.append(actorLoss.scalarized())

            // Optimize value network (critic)
            let (criticLoss, criticGradients) = valueWithGradient(at: self.actorCritic.criticNetwork) { criticNetwork -> Tensor<Float> in
                let stateValues = criticNetwork(oldStates).flattened()
                let loss: Tensor<Float> = 0.5 * pow(stateValues - tfRewards, 2)

                return loss.mean()
            }
            self.criticOptimizer.update(&self.actorCritic.criticNetwork, along: criticGradients)
            criticLosses.append(criticLoss.scalarized())
        }
        self.oldActorCritic = self.actorCritic
        memory.removeAll()
    }
}

Connect The Dots

Now, all that is left to do is to put everything into the training loop. We simply need to run agent.step() at every step and run agent.update() once there is enough experience in the memory.

for episodeIndex in 1..<maxEpisodes+1 {
    var state = env.reset()
    var isDone: Bool
    var reward: Float
    for _ in 0..<maxTimesteps {
        timestep += 1
        (state, isDone, reward) = agent.step(env: env, state: state)

        if timestep % updateTimestep == 0 {
            agent.update()
            timestep = 0
        }

        episodeReturn += reward
        if isDone {
            break
        }
    }
}

We skipped hyperparameter and variable initializations and some logging, but that is all the code we need for Proximal Policy Optimization!

Variable Initialization Code

let env = gym.make("CartPole-v0")
let observationSize: Int = Int(env.observation_space.shape[0])!
let actionCount: Int = Int(env.action_space.n)!

// Hyperparameters
/// The size of the hidden layer of the 2-layer actor network and critic network. The actor network
/// has the shape observationSize - hiddenSize - actionCount, and the critic network has the same
/// shape but with a single output node.
let hiddenSize: Int = 128
/// The learning rate for both the actor and the critic.
let learningRate: Float = 0.0003
/// The discount factor. This measures how much to "discount" the future rewards
/// that the agent will receive. The discount factor must be from 0 to 1
/// (inclusive). Discount factor of 0 means that the agent only considers the
/// immediate reward and disregards all future rewards. Discount factor of 1
/// means that the agent values all rewards equally, no matter how distant
/// in the future they may be. Denoted gamma in the PPO paper.
let discount: Float = 0.99
/// Number of epochs to run minibatch updates once enough trajectory segments are collected. Denoted
/// K in the PPO paper.
let epochs: Int = 10
/// Parameter to clip the probability ratio. The ratio is clipped to [1-clipEpsilon, 1+clipEpsilon].
/// Denoted epsilon in the PPO paper.
let clipEpsilon: Float = 0.1
/// Coefficient for the entropy bonus added to the objective. Denoted c_2 in the PPO paper.
let entropyCoefficient: Float = 0.0001
/// Maximum number of episodes to train the agent. The training is terminated
/// early if maximum score is achieved consecutively 10 times.
let maxEpisodes: Int = 1000
/// Maximum timestep per episode.
let maxTimesteps: Int = 200
/// The length of the trajectory segment. Denoted T in the PPO paper.
let updateTimestep: Int = 1000

var agent: PPOAgent = PPOAgent(
    observationSize: observationSize,
    hiddenSize: hiddenSize,
    actionCount: actionCount,
    learningRate: learningRate,
    discount: discount,
    epochs: epochs,
    clipEpsilon: clipEpsilon,
    entropyCoefficient: entropyCoefficient
)

Full Code for the RL Loop

// Training loop
var timestep: Int = 0
var episodeReturn: Float = 0
var episodeReturns: [Float] = []
var maxEpisodeReturn: Float = -1
for episodeIndex in 1..<maxEpisodes+1 {
    var state = env.reset()
    var isDone: Bool
    var reward: Float
    for _ in 0..<maxTimesteps {
        timestep += 1
        (state, isDone, reward) = agent.step(env: env, state: state)

        if timestep % updateTimestep == 0 {
            agent.update()
            timestep = 0
        }

        episodeReturn += reward
        if isDone {
            episodeReturns.append(episodeReturn)
            if maxEpisodeReturn < episodeReturn {
                maxEpisodeReturn = episodeReturn
                print(String(format: "Episode: %4d | Return: %6.2f", episodeIndex, episodeReturn))
            }
            episodeReturn = 0
            break
        }
    }

    // Break when CartPole is solved for 10 consecutive episodes
    if episodeReturns.suffix(10).reduce(0, +) == 200 * 10 {
        print(String(format: "Solved in %d episodes!", episodeIndex))
        break
    }
}

Conclusion

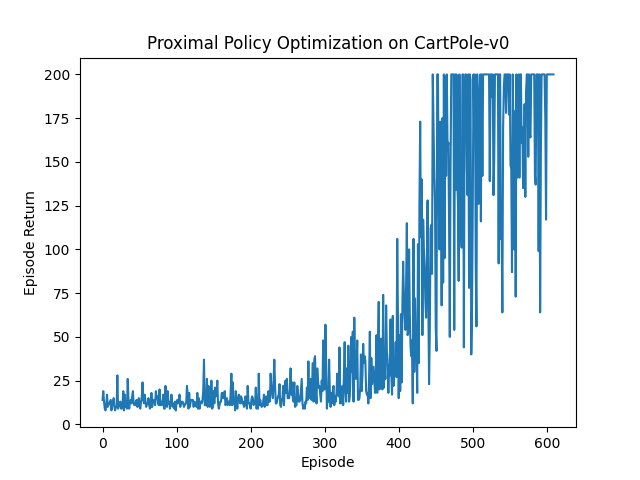
We now have a working Proximal Policy Optimization agent! Like DQN in our previous post, we tested this on CartPole-v0, a simple environment with the goal of balancing a pole on top of a cart by moving the cart left or right. It is a widely used environment for some basic tests, as the environment is simple and the simulator is fast. The maximum cumulative reward is 200.

We train the Proximal Policy Optimization agent until it can reach the maximum score of 200 for 10 consecutive episodes. The agent achieves this goal consistently in less than 1000 episodes.

You can find the entire code at tensorflow/swift-models repository in GitHub and the appropriate PR. Download the code and run swift run Gym-PPO to try it yourself!

endtoend.ai

Train Proximal Policy Optimization (PPO) with Swift for TensorFlow (S4TF)

Introduction

Actor-Critic

Memory

Update Equation

Connect The Dots

Conclusion

Related Posts

Explore →

endtoend.ai

Train Proximal Policy Optimization (PPO) with Swift for TensorFlow (S4TF)

Introduction

Actor-Critic

Memory

Update Equation

Connect The Dots

Conclusion

Related Posts

Train a Deep Q-Network with Swift for TensorFlow (S4TF)

Retrospective of Google Summer of Code 2020 with TensorFlow

Explore →